分数ものさしの作り方や使い方と発売日は？値段と発明者の特許収入も

あなたは小学生のとき、分数の計算は得意でしたか？

分母を揃えたり、分母と分子をひっくり返したり、結構複雑ですよね。

多くの小学生が分数の計算でつまづきます。筆者もそうでしたｗ。

でも、もし直感的に分数の「たし算・ひき算・かけ算・わり算」が計算できる道具があるとしたら、ちょっと気になりませんか。

実はその道具、もうじき商品化されて世に出て来るみたいですよ。

その名も「分数ものさし」。

たった1本、12センチの「分数ものさし」があれば、分数の計算がすぐにできてしまうという画期的な教材とのこと。

発売されたら自分の息子にも買ってあげようかな・・・と考えたので、今回調べてみることにしました。

• 分数ものさしの作り方（自分で作れるのかな？）
• 分数ものさしの使い方（分数計算のやり方）
• 値段（販売価格）
• そして、一体誰が発明したのか
• 発明者には特許料とかガッポガッポ入ってくるのかな・・・^^

なんてことが気になりだしました。

調べてわかったことをあなたにシェアしますね。

近い将来、分数を習う小学生の必須アイテムになるかもしれませんよ。

分数ものさしの作り方は？

出典：http://guide-jp.com/hamamatsu/info/20170407-bunsu

 

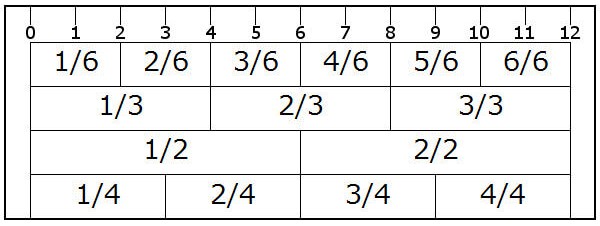
分数ものさしはこんな感じのものです。

目盛なので考え方を押さえれば自分でも作れるかな・・・と考えました。

分数ものさしの作り方を整理してみましょう。

以下の手順でできますよね。

 

ちなみに、ものさしというか定規についてしらべていると、遊び心満載のものもあるのですね。

こんなのをあなたの周りに見せたらきっと「なにこれー、おもしろーい♪」と言われそうな気がします（笑）

おもしろ定規【冗規】使いづらい？でもおもしろい！ペンケースをあけるのが楽しくなる♪あみだ 価格：216円（税込、送料別) (2017/8/19時点)

 

分数ものさしの使い方は？

これ、すごいなぁ。

12歳発案 分数ものさし商品化 – Y!ニュース #Yahooニュースアプリ https://t.co/yIbmFoGjoP

— Sabrina H (@sabrina82h) 2017年8月18日

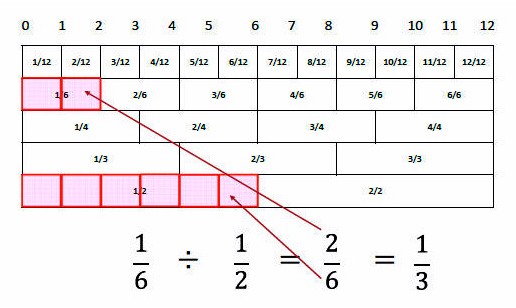
例えば、１／６　÷　１／２ってどう計算しますか？

あなたが習った方法はこうでしよね。

１／６　÷　１／２
＝１／６　☓　２／１
＝２／６
＝１／３

割り算なので「÷１／２」をひっくり返して「☓２／１」としていました。

筆者もそう習ったのですが、もし子供から「なんでひっくり返すの？」とか質問されたらうまく答えらなそう・・・（汗）

これを分数ものさしを使うとなります。

出典：静岡大学、㈲静岡アカデミックリサーチ

定規から、
１／６は、目盛２つ
１／２は、目盛６つ
と数えます。

目盛の数を数えることで２／６、そしたらすぐに１／３と一瞬でできてしまいます。

ポイントは、「目盛を数える」とうことですね。

 

では別の問題に行きますよ。

７／１２　÷　１／４はどうでしょう。

目盛を数えると・・・

７／１２は、目盛７つ
１／４は、目盛３つ

となると、７／３・・・と瞬時に答えが出ますね。

分数ものさしの発売日は？値段も気になる！

分数ものさしは、プレジデントファミリーから発売されています。

ドリルが付いての値段もでていました。

こちらで確認してみてくださいね。

分数ものさし(ドリルつき! ) (【マルチメディア/開発商品】)

 

ドリルの目次はこのようになっていました。

「分数ものさし」でできること

分数ってなんだろう？

分数のおおきさくらべ

同じ大きさなのに数字がちがう？

たし算●2人で走ろう！

ひき算●パン食いきょう走！

かけ算●場所取り合せん！

わり算●山分け作せん！

コラム

●なぜ、「分数ものさし」は「12cm」なの？

●なぜ、たし算・ひき算は通分するの？

●いまは、1年のどれくらい？

●1/5や1/7も計算したい！

●おぼえるひつようがある計算はいくつ？

●かけ算とわり算はどれだけおぼえる？

出典：https://www.amazon.co.jp/exec/obidos/ASIN/4833476797/presidentonline-22/

 

気になる方はこちらで詳細をご確認ください。

 

分数ものさし(ドリルつき! ) (【マルチメディア/開発商品】)

 

 

この他、売れ筋のおもしろ定規としてこんなのを見つけましたよ！

自由スコヤ 四角 定規 折り畳み 筋交付き マルチ 物差し アングル 測定定規 大工道具 プラスチック製

この定規、レビューは例えばこんな感じで評判もよいようです。

このようにamazon（アマゾン）で定規の商品ラインアップを眺めていると、分数ものさしの値段は1,000円もしないかな・・・と筆者は思いました。

なぜなら、分数ものさしは上記でご紹介した折りたたむタイプのものではなく、比較的作りはシンプルですからね。

 

分数ものさしの発明者と特許収入について

分数ものさしを考案したのは、静岡県浜松市在住の山本賢一朗くんです。

当時は、浜松市立神久呂小学校に通っていた５年生でした。

「分数ものさし」の開発に至ったきっかけは、「分数の割り算を友達にわかりやすく教えたい」という思いから、夏休みの自由研究として「分数の教え方」を研究したことです。

商品化には、父親の山本裕一朗さんと静岡大学教育学部の塩田真吾准教授（教育工学）も携わっています。

父親の裕一朗さんは、静岡大大学院生時代に学習塾「静岡アカデミックリサーチ」を起業し現在に至っています。

教育者であり起業家なのですね。

きっと、父親の裕一朗さんの頭には、

• 特許といった権利を押さえる
• 販売権を大手企業に付与
• あとは、売上に応じた特許料を受領

という皮算用があるのではないでしょうか。^^;

もし分数ものさしが爆発的にヒットし、小学生が標準的に持つようになれば、特許料が継続的に入ってきてウハウハだろうなーなんて、勝手に想像してしまいます。

それが実現すれば、父親にとって賢一朗くんは、まさしく「金の卵」ってことになりますかね。

筆者の息子は「金の卵」となってくれるのかな・・・なんて考えるのはやめてきます（笑）

 

まとめ

今回は11月に商品化（製品化）される、「分数ものさし」について調べてみました。

筆者はもういい大人ですから、分数の計算はできます。

でも、子供にわかりやすく教えるとなると話は別。結構難しそう・・・^^;

そんなときに「分数ものさし」があれば、子供の理解も進み、算数が好きになってくれる・・・かもしれませんよね。

ではまた。

この記事を読んだ人はこんな記事も読んでいます

• 「どんたくは雨」のジンクスは2018年も？天気とパレード中止の可能性
• 年末年始高速道路渋滞予測2019！東名の上り下りのピークはいつ？
• こどもちゃれんじのベビーの評判は？口コミも気になる！
• 芦田愛菜の早稲田アカデミーCMまとめ！ロケ地や動画再生回数は？
• 住宅ローン繰り上げ返済のシミュレーション！タイミング効果と注意点